• Home
  • About Street Science
  • Blogposts
  • Get in touch
  • Subscribe
  • Fractals

Science

Calculus (IX): How To Really Understand The Product Rule

Published on October 10, 2022 by Hemanth

Calculus (IX): How To Really Understand The Product Rule - An illustration with whiteboard graphics showing the following information: u(x) = 3x² + 2; v(x) = 2x + 8; y(x) = [u(x)]*[v(x)]; dy/dx = ??
In this 9th calculus series essay, we cover the product rule of differentiation. Learn how to actually use the first principles behind the product rule!
Continue Reading

The Sleeping Beauty Problem: How To Really Solve It?

Published on October 7, 2022 by Hemanth

The Sleeping Beauty Problem: How To Really Solve It? - An illustration that shows the sleeping beauty (stick figure)fast asleep on the right. On her left is a decision flowchart. First, a coin is tossed on Sunday. If the coin lands heads, the flowchart concludes on Monday. If the coin lands tails on Sunday, the experiment is repeated on Monday, and then concluded on Tuesday. What could the sleeping beauty problem be about?
The sleeping beauty problem is a highly controversial decision theory puzzle. It divides experts until this day. Check out what the controversy is all about!
Continue Reading

Fallacy: How To Really Understand It?

Published on October 6, 2022 by Hemanth

How To Really Understand The Notion Of Fallacy? - An illustration showing two stick figures representing two speakers over speaking tables arguing. The stick figure on the left says, "Your logic is weak!" The stick figure on the right asks in return, "How weak is it exactly?"
Fallacy is a term that is often misused in the name of science. This essay explains the formal usage of fallacy and helps you avoid pseudoscientific arguments.
Continue Reading

To Infinity And Beyond? – What Is The Final Destination?

Published on October 5, 2022 by Hemanth

To Infinity And Beyond? - What Is The Final Destination? - An illustration showing white board graphics: limit (t tends to infinity) [Humanity as a function of t = What??]
The phrase “to infinity and beyond” might turn Buzz Lightyear on, but is it the final destination for us? Let us ponder the distant future of humanity and tech!
Continue Reading

Calculus (VIII): How To Learn The Sum Rule And The Difference Rule

Published on October 4, 2022 by Hemanth

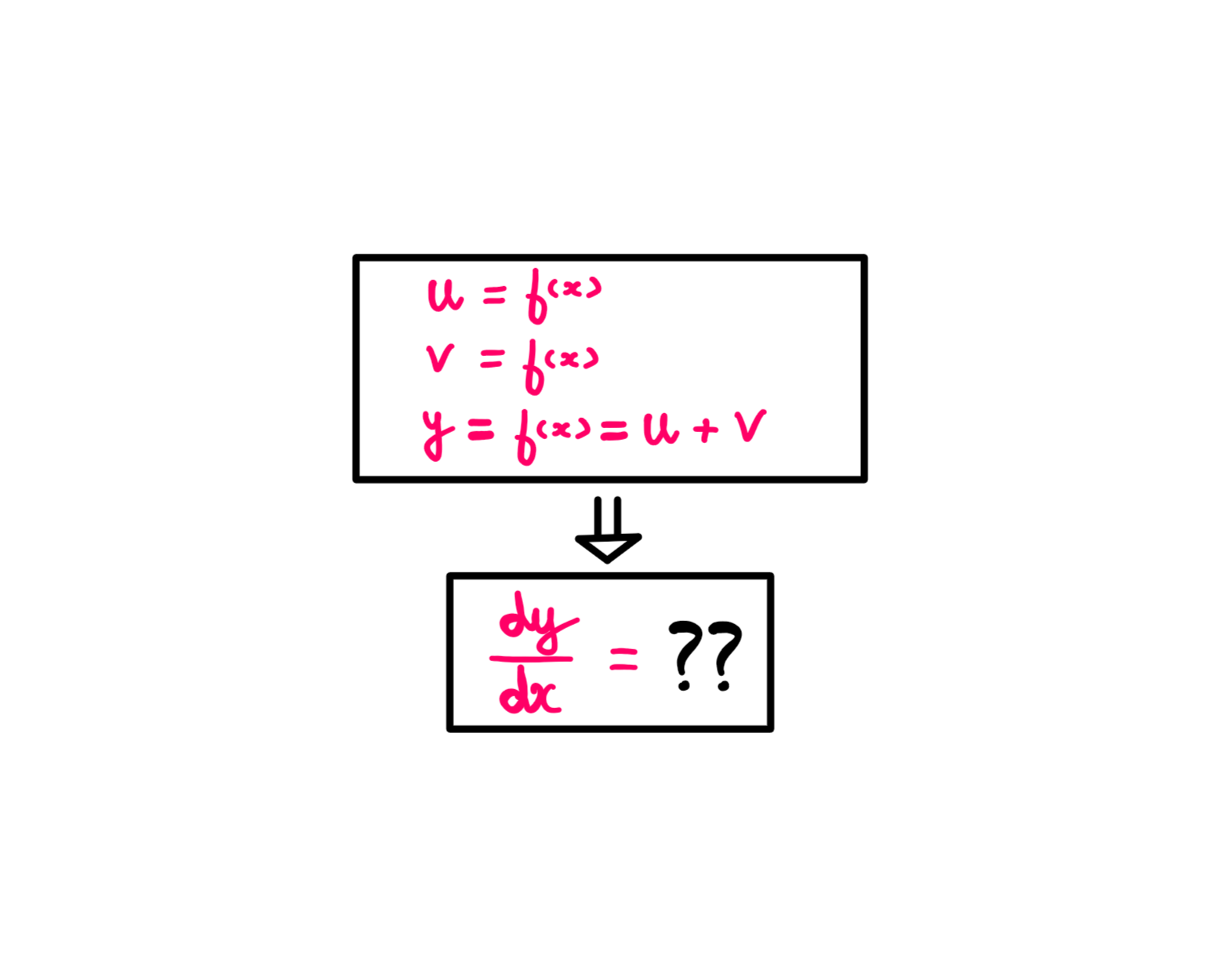
Calculus (VIII): How To Learn Sum Rule And Difference Rule - An illustration showing the following information using white board graphics: u = f(x); v = f(x); y = f(x) = (u + v); → dy/dx = ??
In this 8th calculus essay, you learn the basic math behind the sum rule and the difference rule. Get to know WHY the rules of differentiation actually work!
Continue Reading

Tricky Logic Puzzle (IV): How To Really Solve It?

Published on September 30, 2022 by Hemanth

Tricky Logic Puzzle (IV): How To Really Solve It? - An illustration showing a row five turned-on light bulbs. Beside this row, a robot named "Cheat" appears to be in a puzzled state.
Welcome to the fourth entry in the tricky logic puzzle series. Test your logical reasoning skills with this light bulb puzzle! This time, Cheat is backl!
Continue Reading

Polls Mislead Most Of The Time. Here’s Why.

Published on September 29, 2022 by Hemanth

Polls Mislead Most Of The Time. Here's Why. - A stick figure with an emotionless face holding options A and B on either hand. Above its head floats option C. Two question marks (??) are presented in bubbles as being the thoughts inside the head of the stick figure.
As counterintuitive as it might sound, polls mislead most of the time. This essay explains the math and logic behind this fallacy and how you may avoid it!
Continue Reading

How To Really Solve This Tricky Algebra Problem (VIII)

Published on September 27, 2022 by Hemanth

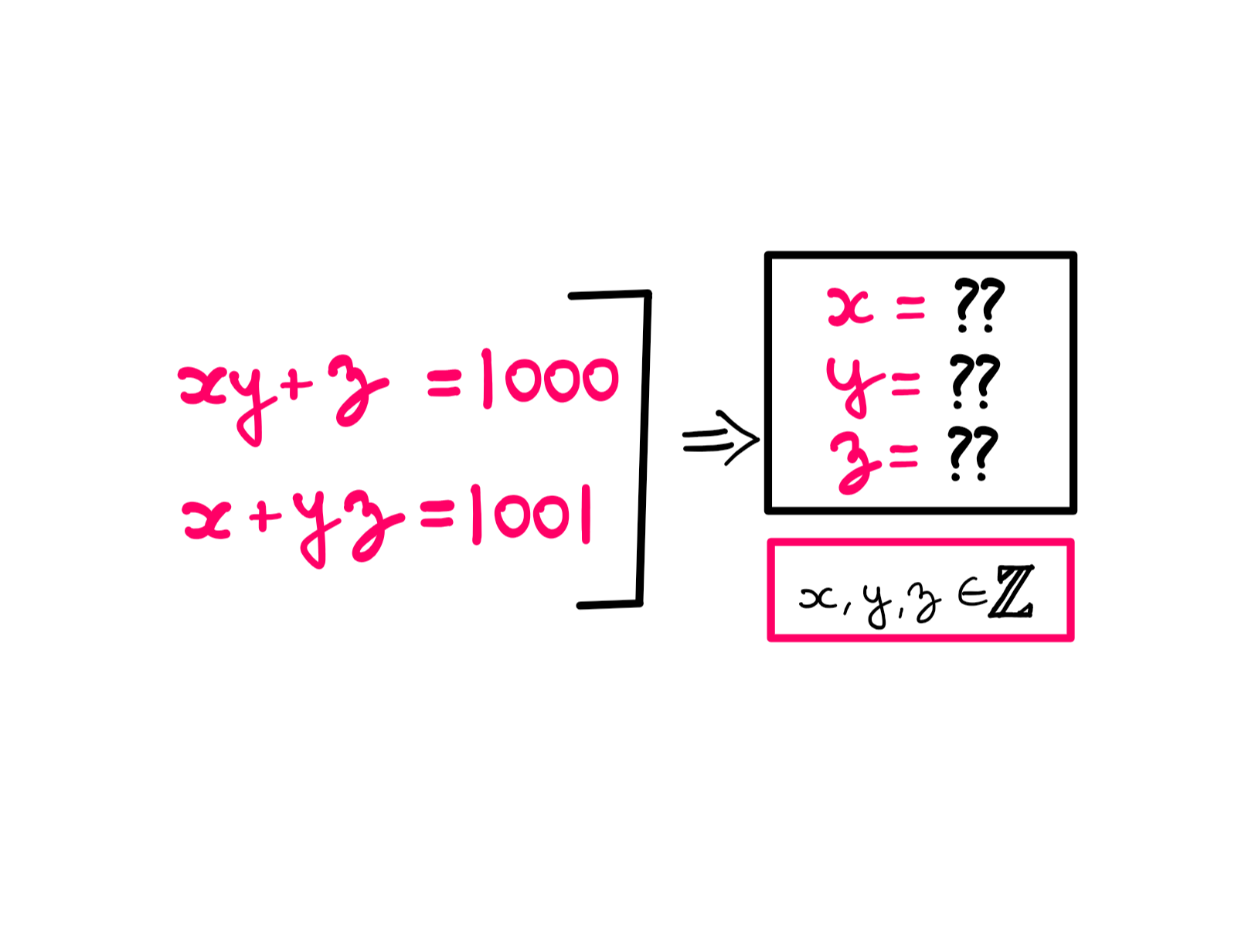
How To Really Solve This Tricky Algebra Problem (VIII) - On the left-hand side, two equations are hand-written: xy + z = 1000; x + yz = 1001; Given these equations, on the right-hand side, the following questions are written down: x = ??; y = ??; z = ?? Below these questions, the author writes that x, y, and z belong to the set of all integers.
The Tricky Algebra Problem Series celebrates the joy of algebra! Problems range from beginner to advanced levels. This one has an easy difficulty level!
Continue Reading

Calculus (VII): How To Differentiate Constants?

Published on September 26, 2022 by Hemanth

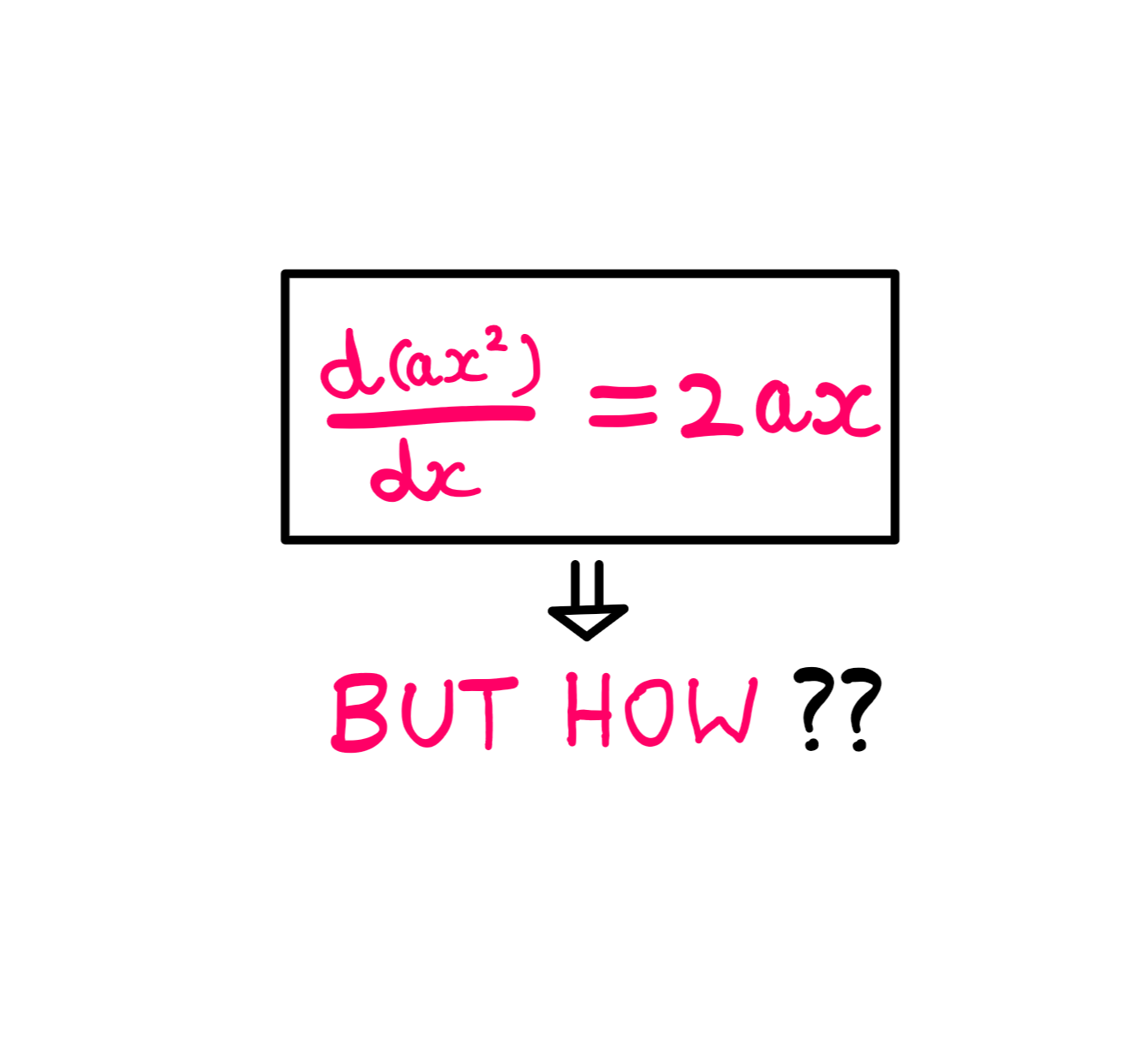
Calculus (VII): How To Differentiate Constants? - An illustration showing that d(ax²)/dx = 2ax. Below this equation, the following question is asked: "But How??"
The seventh entry in the calculus series — an account on how to differentiate constants. This essay uses the product rule to formally differentiate constants.
Continue Reading

Modern Math Is Full Of Symbols. Is This Really Necessary?

Published on September 24, 2022 by Hemanth

Modern Math Is Full Of Symbols. Is This Really Necessary? - On the left is seen, a snippet from Johannes Wildmann's book for merchants. The language is old German. And the snippet seems to suggest 'plus' and 'minus' symbols for the usage of merchants. On the right, the author poses the following question: "How much is too much?"
It is no secret that modern math is full of symbols. Not only does this drive young students away, but even experts face problems. Just how much is too much?!
Continue Reading
  • «
  • 1
  • …
  • 10
  • 11
  • 12
  • 13
  • 14
  • …
  • 35
  • »
© Street Science 2025 - Impressum
We use cookies on our website to give you the most relevant experience by remembering your preferences and repeat visits. By clicking “Accept”, you consent to the use of ALL the cookies.
Cookie SettingsAccept
Manage consent

Privacy Overview

This website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the ...
Necessary
Always Enabled
Necessary cookies are absolutely essential for the website to function properly. These cookies ensure basic functionalities and security features of the website, anonymously.
CookieDurationDescription
cookielawinfo-checkbox-advertisement1 yearSet by the GDPR Cookie Consent plugin, this cookie is used to record the user consent for the cookies in the "Advertisement" category .
cookielawinfo-checkbox-analytics11 monthsThis cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics".
cookielawinfo-checkbox-functional11 monthsThe cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional".
cookielawinfo-checkbox-necessary11 monthsThis cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary".
cookielawinfo-checkbox-others11 monthsThis cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other.
cookielawinfo-checkbox-performance11 monthsThis cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance".
CookieLawInfoConsent1 yearRecords the default button state of the corresponding category & the status of CCPA. It works only in coordination with the primary cookie.
viewed_cookie_policy11 monthsThe cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data.
Functional
Functional cookies help to perform certain functionalities like sharing the content of the website on social media platforms, collect feedbacks, and other third-party features.
Performance
Performance cookies are used to understand and analyze the key performance indexes of the website which helps in delivering a better user experience for the visitors.
CookieDurationDescription
_gat1 minuteThis cookie is installed by Google Universal Analytics to restrain request rate and thus limit the collection of data on high traffic sites.
Analytics
Analytical cookies are used to understand how visitors interact with the website. These cookies help provide information on metrics the number of visitors, bounce rate, traffic source, etc.
CookieDurationDescription
__gads1 year 24 daysThe __gads cookie, set by Google, is stored under DoubleClick domain and tracks the number of times users see an advert, measures the success of the campaign and calculates its revenue. This cookie can only be read from the domain they are set on and will not track any data while browsing through other sites.
_ga2 yearsThe _ga cookie, installed by Google Analytics, calculates visitor, session and campaign data and also keeps track of site usage for the site's analytics report. The cookie stores information anonymously and assigns a randomly generated number to recognize unique visitors.
_ga_R5WSNS3HKS2 yearsThis cookie is installed by Google Analytics.
_gat_gtag_UA_131795354_11 minuteSet by Google to distinguish users.
_gid1 dayInstalled by Google Analytics, _gid cookie stores information on how visitors use a website, while also creating an analytics report of the website's performance. Some of the data that are collected include the number of visitors, their source, and the pages they visit anonymously.
CONSENT2 yearsYouTube sets this cookie via embedded youtube-videos and registers anonymous statistical data.
Advertisement
Advertisement cookies are used to provide visitors with relevant ads and marketing campaigns. These cookies track visitors across websites and collect information to provide customized ads.
CookieDurationDescription
IDE1 year 24 daysGoogle DoubleClick IDE cookies are used to store information about how the user uses the website to present them with relevant ads and according to the user profile.
test_cookie15 minutesThe test_cookie is set by doubleclick.net and is used to determine if the user's browser supports cookies.
VISITOR_INFO1_LIVE5 months 27 daysA cookie set by YouTube to measure bandwidth that determines whether the user gets the new or old player interface.
YSCsessionYSC cookie is set by Youtube and is used to track the views of embedded videos on Youtube pages.
yt-remote-connected-devicesneverYouTube sets this cookie to store the video preferences of the user using embedded YouTube video.
yt-remote-device-idneverYouTube sets this cookie to store the video preferences of the user using embedded YouTube video.
Others
Other uncategorized cookies are those that are being analyzed and have not been classified into a category as yet.
CookieDurationDescription
_learn_press_session_a7b7f6513d11f58744fec86fbc57b1162 daysNo description
_wordpress_lp_guest1 hourNo description
GoogleAdServingTestsessionNo description
SAVE & ACCEPT
Powered by CookieYes Logo
af Afrikaansar Arabiczh-CN Chinese (Simplified)nl Dutchen Englishfr Frenchde Germanhi Hindiit Italianja Japanesept Portugueseru Russianes Spanishta Tamil
en English